f(x)=(cx+d)!(ax+b)!
- a<c
显然 x 趋于无穷时,分子和分母皆为无穷大量
而分母的阶大于分子的阶(分母比分子快),故 limx→+∞f(x)=0
又 x 充分大时,f(x) 递减
故 n=0∑∞(cx+d)!(ax+b)! 收敛
- eg. f(x)=(2x−1)!(x+1)!
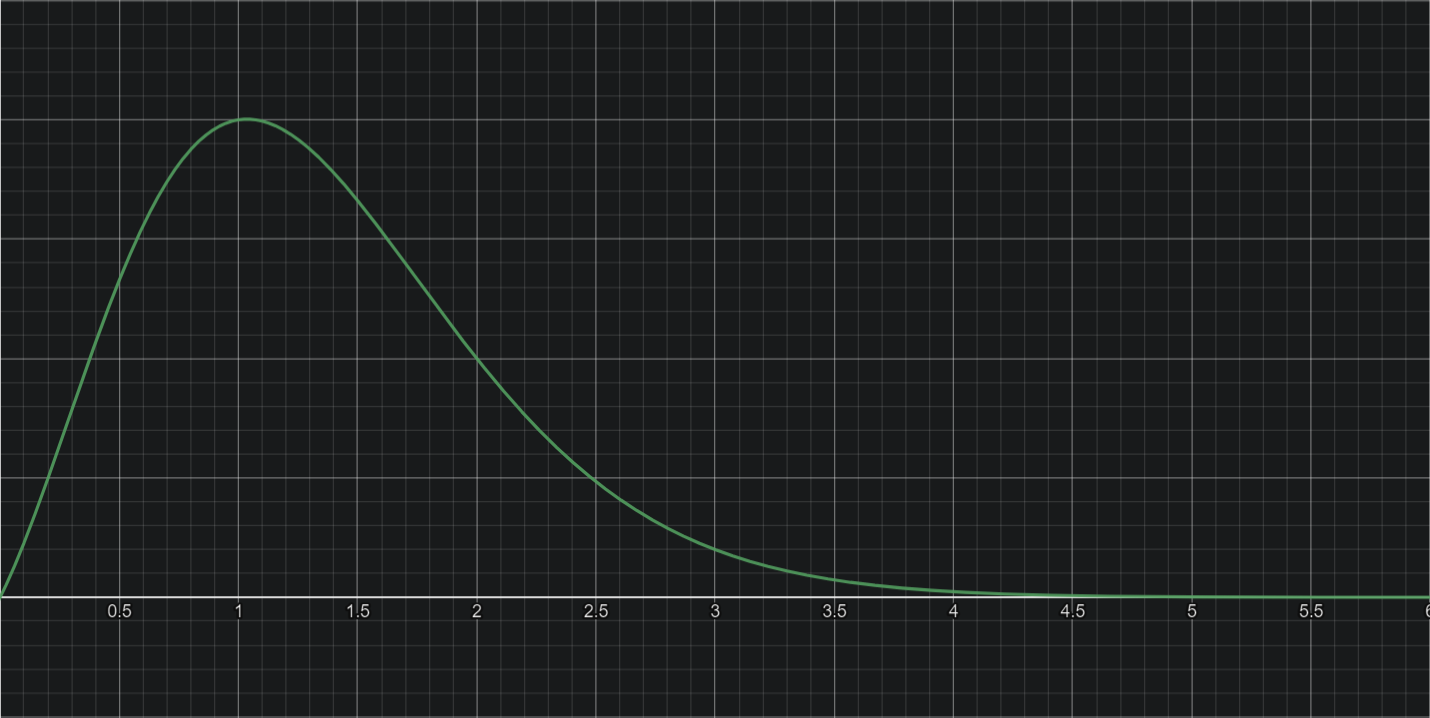
- a=c 且 b<d
显然 x 趋于无穷时,分子和分母皆为无穷大量
而分母的阶大于分子的阶(分母比分子快),故 limx→+∞f(x)=0
又 x 充分大时,f(x) 递减
故 n=0∑∞(cx+d)!(ax+b)! 收敛
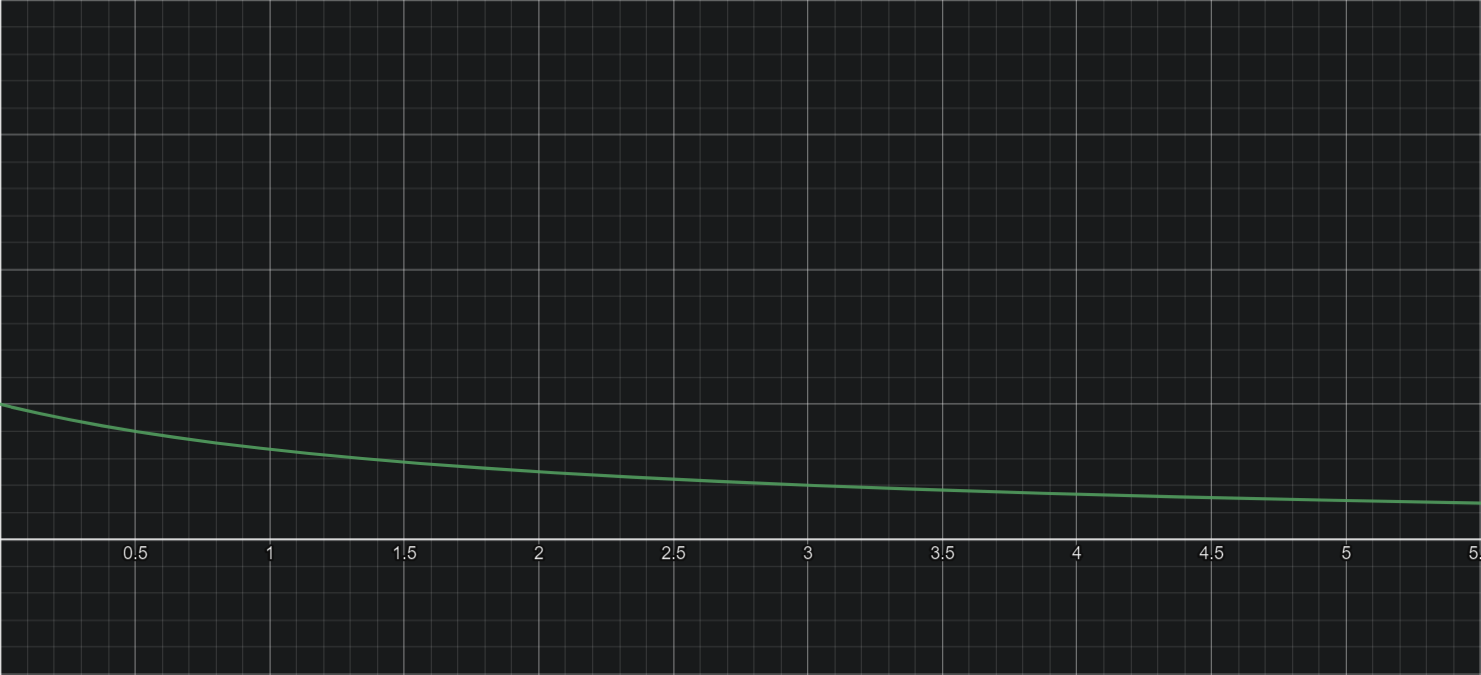
- eg. f(x)=(x+2)!(x+1)!
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ZouWeiyi's Home!



